g. Rostova-na-Donu, Russian Federation
student
This article presents a statistical analysis of the cost of a conditional (minimum) set of food products in the Rostov region. Econometric modeling using adaptive methods of the time series of the cost indicator is carried out based on monthly data for the period from January 2015 to September 2025 in the Rostov region. Using the obtained models, a forecast of the cost of a minimum set of food products for October-December 2025 was made. The final result is specified as the average of the three forecasts
time series, econometricmodel,forecasting,the cost of a conditional (minimum) set of food, adaptive methods, exponential smoothing, regression
Одним из ключевых индикаторов статистики потребительских цен является стоимость условного (минимального) набора продуктов питания. Этот показатель отражает различия в уровне цен на продовольственные товары между регионами.
Любое государство использует понимание человеческих потребностей для формирования эффективной социально-экономической политики, например, обеспечивает доступность продуктов питания.Так Правительство Российской Федерации вправе устанавливать предельные розничные цены на определенные категории товаров, имеющих важное социальное значение и являющихся предметами первой необходимости. К таким товаром можно отнести 24 продовольственных продукта [1].
Также на законодательном уровне, а именно приложением 4 Приказа Росстата от 19.12.2024 № 657 «Об утверждении наборов потребительских товаров и услуг и перечня базовых городов Российской Федерации для наблюдения за ценами и тарифами», установленпереченьтоваровусловного набора продуктов питания.В него входит 33 продовольственных товара, в числе которых можно выделить следующие категории: хлеб, мясо, молочные продукты,яйца, фрукты,овощи, крупы, чай, сахар, соль и специи.Если сравнить минимальный набор продуктов питания и перечень социально значимых товаров первой необходимости, то можно прийти к выводу, что эти списки совпадают. Правительство Российской Федерации,таким образом, ограничивает рост цен.
Стоимость условного набора продуктов анализируется с целью сопоставления стоимости наборов между регионами России в длительной динамике. Количество товаров в наборе является условным, и оно не отражает реальное потребление продуктов населением.Таким образом, состав и объём набора не варьируется в зависимости от региона, поэтому исследованию подлежит только динамика цен.Данные о стоимости набора определяются в расчёте на одного человека в месяц на основе официальной статистической методологии, утверждённой приказом Росстата [2].
Актуальность данного исследования обусловлена тем, что результаты исследования имеют практическое значение для составления бюджета домохозяйств, помогают дать оценку уровня инфляции и сформировать региональную социально-эконмическую политику.
На данную тематику можно найти прогнозирование стоимости минимального набора продуктов питания для Владимирской и Саратовской области,Республики Марий Эл, но нет исследования по этому показателю для Ростовской области[3–5]. Это также доказывает актуальность выбранной темы.
Целью данной статьи является построение моделей для прогнозированиястоимости условного (минимального) набора продуктов питания в Ростовской области на октябрь, ноябрь и декабрь 2025 годаэконометрическими методами на основе помесячных данных этого показателя с января 2015 года по сентябрь 2025 года (табл. 1).
Таблица 1
Стоимость минимального набора продуктов питания в Ростовской области по месяцам с января 2015 по сентябрь 2025 гг., тыс. руб.[6]
t Yt t Yt t Yt t Yt t Yt t Yt
1 3,339 23 3,387 45 3,484 67 4,072 89 6,003 111 5,763
2 3,477 24 3,408 46 3,506 68 3,967 90 5,789 112 5,784
3 3,502 25 3,429 47 3,560 69 3,916 91 5,365 113 5,988
4 3,519 26 3,440 48 3,677 70 3,963 92 5,225 114 6,255
5 3,583 27 3,456 49 3,749 71 4,039 93 5,156 115 6,290
6 3,562 28 3,538 50 3,765 72 4,170 94 5,170 116 6,278
7 3,470 29 3,779 51 3,834 73 4,236 95 5,167 117 6,194
8 3,287 30 3,885 52 3,876 74 4,291 96 5,223 118 6,334
9 3,247 31 3,658 53 4,038 75 4,420 97 5,272 119 6,552
10 3,266 32 3,473 54 3,989 76 4,508 98 5,324 120 6,712
11 3,296 33 3,392 55 3,885 77 4,626 99 5,305 121 6,874
12 3,336 34 3,382 56 3,785 78 4,832 10 5,388 122 7,039
13 3,380 35 3,375 57 3,735 79 4,607 101 5,602 123 7,288
14 3,391 36 3,390 58 3,708 80 4,499 102 5,669 124 7,622
15 3,394 37 3,453 59 3,708 81 4,572 103 5,617 125 7,775
16 3,408 38 3,503 60 3,738 82 4,812 104 5,468 126 7,629
17 3,489 39 3,570 61 3,794 83 4,890 105 5,463 127 7,273
18 3,537 40 3,599 62 3,802 84 4,964 106 5,475 128 6,855
19 3,478 41 3,596 63 3,855 85 5,129 107 5,530 129 6,846
20 3,421 42 3,666 64 3,987 86 5,175 108 5,597
21 3,364 43 3,609 65 4,079 87 5,717 109 5,656
22 3,371 44 3,537 66 4,168 88 5,926 110 5,720
На основе данных, представленных в табл. 1, построим график временного ряда показателя стоимости условного набора продуктов питания в Ростовской области (рис. 1). Число наблюдений равно 129.

Рис. 1. Динамика стоимости минимального набора продуктов питания в Ростовской областис линией тренда, тыс. руб. [6]
График рядадемонстрирует увеличение показателя стоимости, причём, максимальное значение приходится на май-июнь, а минимальное – чаще всего на сентябрь. По состоянию на сентябрь 2025 года прирост стоимости минимального набора продуктов питания в Ростовской области составил 105,02% относительно января 2015 года, т.е. стоимость увеличилась более чем в 2 раза.Причиной таких изменений мог послужить рост уровня инфляции и повышение издержек производителей, ажиотажный спрос, изменение в государственной политике, сезонные и внешние факторы, такие как неурожаи, коронавирусная инфекция, санкции и сбои в логистике.
В условиях возрастающей подвижности социально-экономических систем для моделирования требуются методы, способные оперативно реагировать на изменения.Для нахождения прогнозной стоимости минимального набора продуктов питания в Ростовской областииспользуем адаптивные методы прогнозирования.Ихсущность – построение самокорректирующейся модели, способной учитывать результаты предыдущих прогнозов.
Одним из наиболее часто применяемых адаптивных методов прогнозирования является экспоненциальное сглаживание, поэтому вначале используем его.
Для экспоненциального сглаживания приведём следующую формулу (1):
S_t= S_(t-1)+α·(y_t-S_(t-1)), (1)
гдеSt– значениесглаженнойэкспоненциальной средней в момент времени t;
St-1 – предыдущее сглаженное значение;
yt– показатель текущего наблюдения;
α – параметр сглаживания, причём, α = const, 0< α<1.
При краткосрочномоперативном прогнозировании для параметра адаптации α присваивают значение, близкое к единице, поэтому установим, что значение α = 0,8.
В качестве начального значения S0примем среднее арифметическое значение из всех данных уровней временного ряда. Определим:
S_0=((3,339+3,477+⋯+6,846))/129= 4,537.
Вычислим по формуле (1) экспоненциальные средние и с помощью графика сравним их с исходным временный рядом (рис. 2).

Рис. 2. Графики исходного и экспоненциально сглаженного ряда
Полученныеграфики исходного и экспоненциально сглаженного ряда практически совпадают, это свидетельствует о минимальном влиянии случайных шумов на исходные данные, то есть отсутствуют выбросы, которые могли бы исказить прогноз. Поэтому с помощью модели экспоненциального сглаживания (1) вычислим первое прогнозное значение – на октябрь 2025 года:
(Y_130 ) ̂=6,867+0,8·(6,846-6,867)= 6,84997 тыс.руб.
Аналогично рассчитаем прогнозное значение на ноябрьи декабрь. Они будут равны6,85066 тыс. руб. и 6,85077 тыс. руб. соответственно.
Таким образом, метод экспоненциального сглаживания довольно прост в использовании и доступен в понимании, он корректирует подъёмы и спады, происходящие в определённые периоды времени. Порезультатам прогнозирования можно предположить, что стоит ожидать незначительный рост стоимости минимального набора продуктов питания.
Решение задачипрогнозированиявозможно и при помощи регрессионного анализа. Предварительно сделав замену, применяем средство «Пакет анализа» Microsoft Excel (инструмент «Регрессия») для получения уравнения регрессии и регрессионной статистики. В итоге получим уравнение в виде квадратичного уравнения регрессии(2):
(Y_t ) ̂= 3,497 - 0,011·t + 0,00031·t2, (2)
с регрессионной статистикой, представленной на рис. 3.
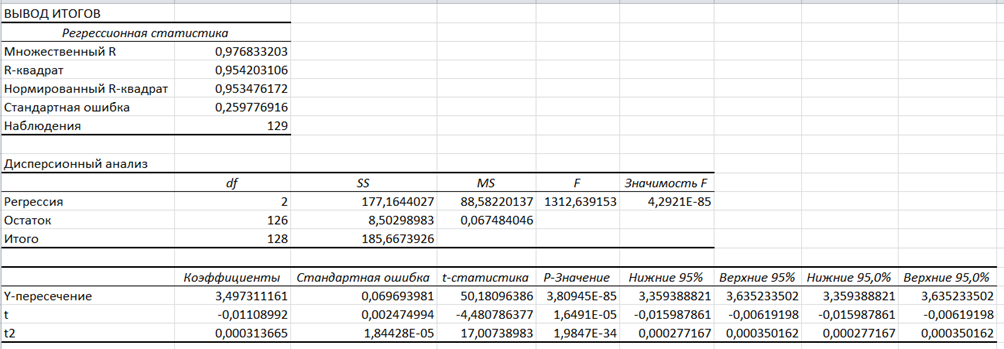
Рис. 3. Вывод итогов регрессионного анализа
Расчётное значение статистики Фишера F = 1 312,64 больше табличного и статистически значимо (4,2921Е-85 < 0,05). Коэффициенты модели (2) также значимы. С помощью теста Дарбина-Уотсона установлено, что автокорреляция в остатках отсутствует.
С помощью уравнения регрессии(2) вычислим прогнозное значение на октябрь 2025 года:
(Y_130 ) ̂=3,497 - 0,011·130 + 0,00031·130^2= 7,35655 тыс.руб.
Прогнозное значение на ноябрьсоставит 7,42733тыс. руб., а на декабрь – 7,49873тыс. руб.
Таким образом, квадратичное уравнение регрессии позволяет предсказывать значения объясняемой переменной (Y_t ) ̂ на основе значений объясняющих переменных t и t2, учитывая, как изменение периода времени влияет нелинейным образом.
При этом для увеличения точности прогнозов исследуемого показателя в изменяющихся условиях необходима работа по совершенствования моделей. Важную роль в этом играют адаптивные методы прогнозирования. Адаптивные модели прогнозирования отличаются от других прогностических моделей тем, что они отражают текущее состояние временного ряда и учитывают развитие динамических характеристик изучаемого процесса [7, c. 7].
Для временного ряда из табл. 1 наилучшим образом применима адаптивная полиномиальная модель второго порядка, которая описывается уравнениемвида (3):
y ̂_τ (t)=a ̂_(1,t)+τ∙a ̂_(2,t)+1/2∙τ^2∙a ̂_(3,t). (3)
Коэффициенты данной модели a ̂_(1,t), a ̂_(2,t), a ̂_(3,t)обновляются на каждом последующем шаге по формулам:
a ̂_(1,t)=3∙(S_t^((1) )-S_t^((2) ) )+S_t^((3) );
a ̂_(2,t)=α/(2β^2 )∙[(6-5α)∙S_t^((1) )-2(5-4α)∙S_t^((2) )+(4-3α)∙S_t^((3) ) ];
a ̂_(3,t)=α^2/β^2 ∙(S_t^((1) )-2∙S_t^((2) )+S_t^((3) )).
Используя уравнение тренда (2),в качестве начальных условий положим:a ̂_1,0=3,497; a ̂_2,0=-0,011;a ̂_3,0=0,0003.Выберем методом проб параметр адаптации α = 0,8, β = 1 – α = 0,2. Такое высокое значение α указывает на придание наибольшего веса последним наблюдениям ряда, что критически важно для улавливания резких изменений в современных условиях.
S_0^((1))=a ̂_1,0-β/α∙a ̂_2,0+β(2-α)/(2α^2 )∙a ̂_3,0=3,4998;
S_0^((2))=a ̂_1,0-2β/α∙a ̂_2,0+β(3-2α)/α^2 ∙a ̂_3,0=3,5026;
S_0^((3))=a ̂_1,0-3β/α∙a ̂_2,0+3β(4-3α)/(2α^2 )∙a ̂_3,0=3,5055.
Проведём вычисление экспоненциальных средних с помощью рекуррентных формул:
S_t^((1))=α∙y_t+β∙S_(t-1)^((1) ); (6)
S_t^((2) )=α∙S_t^((1) )+β∙S_(t-1)^((2) ); (7)
S_t^((3))=α∙S_t^((2) )+β∙S_(t-1)^((3) ). (8)
Выполним расчёт экспоненциальных средних с применением формул (6)–(8). Результат вычислений представлен на рис. 4.

Рис. 4. Результаты расчёта экспоненциальных средних
Находим оценки коэффициентов модели (3):
a ̂_1,129=6,8411;
a ̂_2,129=0,0081;
a ̂_3,129=0,1502.
Используем для прогнозирования полиномиальную модель (3) и получим:
(Y_t ) ̂ = 6,8411 + 0,0081·τ + 0,5·0,1502·τ2.
Прогноз на октябрь-декабрь 2025 года:
(Y_130 ) ̂ = 6,8411 + 0,0081 + 0,5·0,1502=6,92432 тыс.руб.
(Y_131 ) ̂ = 6,8411 + 0,0081·2 + 0,5·0,1502·4=7,15778 тыс.руб.
(Y_132 ) ̂ = 6,8411 + 0,0081·3 + 0,5·0,1502·9=7,54147 тыс.руб.
Таким образом, использование адаптивной полиномиальной модели требует множества расчётов, однако даёт наиболее точный результат. Он получился больше значения, полученного путём экспоненциального сглаживания, но меньше, чем при регрессионном анализе.
Для повышения точности прогноза найдём среднеарифметическое значение полученных значений, а уточнённый результат представим в виде табл. 2.
Таблица 2
Скорректированноепрогнозное значение стоимости минимального набора продуктов питания в Ростовской области, тыс. руб.
Период Метод экспоненциального сглаживания Регрессионный анализ Адаптивная полиномиальная модель Уточнённое значение
Октябрь 6,84997 7,35655 6,92432 7,04361
Ноябрь 6,85066 7,42733 7,15778 7,14526
Декабрь 6,85077 7,49873 7,54147 7,29699
Таким образом, в 2025 г. в Ростовской области прогнозируется следующая динамика стоимости условного набора продуктов питания: в октябре цена может составить 7 043,61 руб., в ноябре – 7145,26 руб., а в декабре – 7 296,99 руб. К концу года цены вырастут примерно на 6,59% процентов.
Напомним, что минимальный набор продуктов на человека является условным и не отражает реального потребления населением. Его цель – это анализ динамики стоимости продуктов в регионах.
Показатель стоимости условного (минимального) набора продуктов питания отражает изменения в цене на набор потребляемых товаров при условии его неизменности и ограничения минимальным количеством. Прогнозирование этого показателя позволяет контролировать финансовое положение различных групп населения, что важно для поддержания устойчивого состояния региональной экономики.
1. Resolution of the Government of the Russian Federation of July 15, 2010 No. 530 "On approval of the Rules for establishing maximum permissible retail prices for certain types of socially significant essential food products, a list of certain types of socially significant essential food products for which maximum permissible retail prices may be established, and a list of certain types of socially significant food products for the purchase of a certain quantity of which a business entity engaged in trading activities is not allowed to pay remuneration" (as amended on February 1, 2025) //SPS "ConsultantPlus". URL: https://www.consultant.ru/document/cons_doc_LAW_102841/.
2. Order of Rosstat dated 15.12.2021 No. 915 "On approval of the Official Statistical Methodology for monitoring consumer prices for goods and services and calculating consumer price indices" (as amended on 22.07.2022) // SPS "ConsultantPlus". URL: https://www.consultant.ru/document/cons_doc_LAW_404082/d1df0f7ecce5a8efe975983c6fbb85f346a9006e/.
3. Bukhnaeva P.A., Dergousova A.A. Modeling the cost of a conditional (minimum) set of food products in the Vladimir region // Collection of student research papers for the 2022/23 academic year. 2023. pp. 298–310.
4. Grakholskaya L.V., Mitrofanov A.Yu. Forecasting the Dynamics of the Cost of a Minimum Set of Food Products // Bulletin of the Saratov State Socio-Economic University. 2016. Pp. 86–90.
5. Faskhudinova Yu.V. Statistical Analysis of the Cost of a Conditional (Minimum) Set of Food Products // Collection of Materials of the Student Scientific Conference Based on the Results of R&D "Students – Innovations – Economy of Modern Russia". 2022. Pp. 1–6.
6. Cost of a Conditional (Minimum) Set of Food Products. Indicator Passport // EMISS. State Statistics. URL: https://www.fedstat.ru/indicator/31481.
7. Lukashin Yu.P. Adaptive Methods of Short-Term Forecasting of Time Series: A Tutorial. Moscow: Finance and Statistics, 2003. 416 p.
Authors: Kudryavtsev Oleg








