ОЦЕНКА ОБЪЕМОВ ТОВАРООБОРОТА РОССИИ СО СТРАНАМИ ЕАЭС

Цвиль Мария Михайловна; Шарлай А. Н.

doi:doi:10.26526/2307-9401-2024-2-11-15

Главная / Журналы / Наука и мир / Номер 2 / ОЦЕНКА ОБЪЕМОВ ТОВАРООБОРОТА РОССИИ СО СТРАНАМИ ЕАЭС

Отправить рукопись Скачать PDF
Текст

Цитировать

Цитирований:

ОЦЕНКА ОБЪЕМОВ ТОВАРООБОРОТА РОССИИ СО СТРАНАМИ ЕАЭС

Журнал: НАУКА И МИР № 2 , 2024

Рубрики: ЭКОНОМИЧЕСКИЕ НАУКИ

УДК 330.43 Эконометрия ГРНТИ 06.00 ЭКОНОМИКА И ЭКОНОМИЧЕСКИЕ НАУКИ

Цвиль Мария Михайловна ¹

Шарлай А. Н. ²

Информация об авторах и публикации

Авторы:

1. Российская таможенная академия (Информатика и информационные таможенные технологии, доцент)

г. Ростова-на-Дону, Россия

2. Ростовский филиал Российской таможенной академии

Тип:

Статья

DOI:

https://doi.org/10.26526/2307-9401-2024-2-11-15

Страницы:

с 11 по 15

Статус:

Опубликован

Получено:

20.11.2024

Одобрено:

20.11.2024

Опубликовано:

04.12.2024

Классификаторы:

УДК 330.43 Эконометрия
ГРНТИ 06.00 ЭКОНОМИКА И ЭКОНОМИЧЕСКИЕ НАУКИ

Язык материала:

русский

Ключевые слова:

товарооборот, временной ряд, эконометрическое моделирование, адаптивные методы, экспоненциальное сглаживание, прогноз

Аннотация и ключевые слова

Аннотация (русский):
В статье исследуется динамика объемов взаимной торговли стран ЕАЭС и оценивается удельный вес государств-членов ЕАЭС в ней. Проводится эконометрическое моделирование адаптивными методами объемов товарооборота России в ЕАЭС по месячным данным с января 2015 по декабрь 2021 года. Для построения прогнозных моделей используется экспоненциальное сглаживание и полиноминальная модель первого порядка Брауна

Ключевые слова:
товарооборот, временной ряд, эконометрическое моделирование, адаптивные методы, экспоненциальное сглаживание, прогноз

Текст

Текст (PDF): Читать Скачать

В условиях глобализации невозможно представить систему мирового хозяйства без интеграционных объединений различного уровня. Глубокие интеграционные процессы развиваются по всему миру от Латинской Америки до Азиатско-Тихоокеанского региона, это связано с тем, что экономический потенциал интеграционных блоков намного выше отдельных национальных систем в разрезе постоянного противостояния вызовам глобальной конкуренции. Так, к основным целям создания Евразийского экономического союза (ЕАЭС) можно отнести: укрепление национальных экономик и возможностей государств–членов в мировой с учетом создания возможности свободного передвижения товаров, услуг, финансов и рабочей силы.

Российская Федерация, как ключевой член ЕАЭС, выступает за усиление интеграционных связей в Евразийском регионе путем развития Союза и заключения внешнеторговых соглашений с третьими странами, так как это может способствовать формированию региона, привлекательного для других экономических игроков. Кроме того, одним из явных преимуществ ЕАЭС для экономики России является устойчивость, позволяющая даже в условиях нестабильности экономической ситуации сохранять положительную динамику роста и сглаживать негативные последствия политического влияния.

Евразийская экономическая комиссия (ЕЭК) ежегодно формирует статистические данные, позволяющие оценить состояние и динамику взаимной торговли между государствами-членами, а также удельный вес товарооборота каждой из стран-участниц Союза.

Цель статьи ― провести эконометрическое моделирование объемов товарооборота России со странами ЕАЭС с целью прогнозирования. В настоящее время в большинстве исследований недостаточно используется эконометрическое моделирование. В рамках данной статьи продемонстрирован эконометрический подход к моделированию временного ряда по данным об объемах товарооборота России со странами ЕАЭС.

В соответствии с брошюрой, подготовленной Департаментом статистики ЕЭК в 2022 году к десятилетию евразийской интеграции, а также статистическим ежегодником ЕАЭС в таблице 1 приводятся данные об объемах взаимной торговли товарами между странами Союза в 2015–2021 гг [1].

Таблица 1

Взаимная торговля товарами государств – членов ЕАЭС (миллиардов долларов США) (объем экспортных операций во взаимной торговле)

	2015	2016	2017	2018	2019	2020	2021
ЕАЭС	45,6	43,0	54,7	60,3	61,6	55,1	73,1
Армения	0,3	0,4	0,6	0,7	0,8	0,7	0,9
Беларусь	11,0	11,4	13,6	13,9	14,6	14,0	17,4
Казахстан	5,1	3,9	5,3	6,1	6,4	5,7	7,8
Кыргызстан	0,4	0,5	0,5	0,6	0,6	0,6	0,8
Россия	28,8	26,8	34,7	39,0	39,2	34,1	46,2

На основании информации, представленной в табл. 1, можно построить диаграммы, отражающие динамику взаимной торговли(рис.1), а также удельный вес в ней каждого из государств-членов(рис.2).

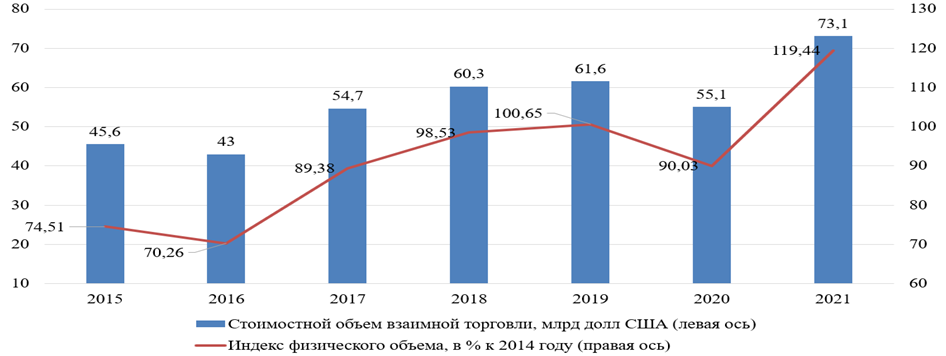
Рис.1.Динамика взаимной торговли товарами ЕАЭС

На рисунке 1 показано, что в целом наблюдается наращивание объемов взаимной торговли ЕАЭС.Можно отметить значительное влияние кризиса2020 года, вызванного пандемией COVID-19 и ухудшением внешнеторговой конъюнктуры, как на объем товарооборота ЕАЭС, так и отдельных стран-участниц.Так, исходя из данных табл.1 объем торговли товарами России во взаимной торговле в 2020 году снизился с 39,2 млрд долл. США до 34,1 млрд долл. США, что составляет 86,9% по отношению к предыдущему году.

Рис.2.Удельный вес государств-членов ЕАЭС в объеме взаимной торговли товарами (в процентах)

Исходя из полученных графических данных, можно сделать вывод, что с момента создания ЕАЭС и по 2021 год включительно основной удельный вес в объемах взаимной торговли занимает Российская Федерация, на ее долю приходится более 60% объемов товарооборота Союза, что определяет ее ключевую позицию внутри интеграционного блока.

В аналитическом докладе за 2022 год отмечается положительная динамика роста взаимной торговли, которая была обеспечена переориентацией торговых потоков в ответ на введение в 2022 году рядом третьих стран ограничений в отношении экспортно-импортных операций с Беларусью и Россией, а также ростом внутреннего производства в отдельных отраслях [1]. Так, объём взаимной торговли по итогам января – сентября 2022 года достиг 58,5 млрд долл. США, что на 11,9% выше, чем в сопоставимом периоде 2021 года.В своем докладе Михаил Мишустин, председатель Правительства РФ, в рамках заседания на стратегической сессии "Евразийская интеграция в многополярном мире" отметил, что в 2023 году товарооборот внутри ЕАЭС стал рекордным с момента его учреждения в 2014 году — 7,4 трлн руб., увеличившись вдвое.

Однако на фоне введения санкций против России во избежание некорректных оценок, спекуляций и разночтений официальная статистическая информация об объемах внешней и взаимной торговли с итогов за январь-февраль 2022 года отнесена к сведениям ограниченного распространения и не подлежит публикации. В связи, с чем экономико-статистический анализ взаимной торговли возможен лишь на основе помесячных данных за период с января 2015 года по декабрь 2021 года включительно.

Опубликованные ежегодно Комиссией ЕЭК статистические таблицы с помесячной информацией стоимостных объемов товарооборота внутри ЕАЭС можно представить в виде одномерного временного ряда.

Таблица 2

Данные объема товарооборота России в ЕАЭС (млн. долл. США)

год	t	Y млн. $	год	t	Y млн. $	год	t	Y млн. $	год	t	Y млн. $
2015	1	1827,158	2017	25	2334,192	2019	49	2527,129	2021	73	2676,561
	2	2369,036		26	2464,230		50	2869,248		74	3061,799
	3	2571,135		27	2767,806		51	3247,673		75	3740,545
	4	2806,510		28	2688,230		52	3458,746		76	3905,028
	5	2456,185		29	2881,259		53	2895,918		77	3691,417
	6	2447,640		30	2935,431		54	3102,474		78	3799,209
	7	2446,683		31	2705,122		55	3326,162		79	3917,834
	8	2389,112		32	2910,780		56	3400,873		80	3975,946
	9	2308,991		33	3029,095		57	3449,150		81	4207,475
	10	2426,439		34	3278,049		58	3359,669		82	4183,234
	11	2341,231		35	3243,725		59	3722,081		83	4521,834
	12	2431,049		36	3447,622		60	3888,091		84	4478,607
2016	13	1675,368	2018	37	2744,127	2020	61	2486,688
	14	1883,765		38	3136,585		62	2707,933
	15	2236,375		39	3317,939		63	2600,382
	16	2244,330		40	3239,806		64	2126,281
	17	2192,248		41	3238,452		65	2461,564
	18	2341,126		42	3336,128		66	2967,498
	19	2015,030		43	3221,960		67	2984,597
	20	2186,594		44	3425,714		68	2735,248
	21	2332,825		45	3229,057		69	3032,824
	22	2484,521		46	3571,221		70	3239,787
	23	2482,835		47	3281,877		71	3227,278
	24	2729,303		48	3210,528		72	3538,517

В связи с тем, что в последние годы наблюдается возрастание подвижности социально-экономических систем, то для моделирования в таких условиях лучше применять методы, которые быстро реагируют на изменение условий. К таким методам относятся адаптивные методы, которые позволяют строить самонастраивающиеся математические модели. В нашей статье для построения прогнозной модели используем различные адаптивные методы. Самым простым из них является экспоненциальное сглаживание. Поэтому используем вначале этот метод. Проведем экспоненциальное сглаживание данного ряда (табл.2).

Экспоненциальное сглаживание экстраполирует значения временного ряда на основе расчёта экспоненциальных скользящих средних сглаживаемого ряда, при этом вес (степень влияния) данных в анализе уменьшается по мере их устаревания.Общая формула расчета экспоненциальной средней имеет вид [2]:

, (1)

где ― значение экспоненциальной средней в момент t; ― параметр сглаживания,

В качестве начального значения S₀ возьмем среднее арифметическое значение из всех данных уровней временного ряда. Экспериментальным методом установим, что значение параметра адаптации α = 0,8. На основе вычисленных экспоненциальных средних сравним графически исходный временной ряд и экспоненциально сглаженный по формуле (1) (рис.3).

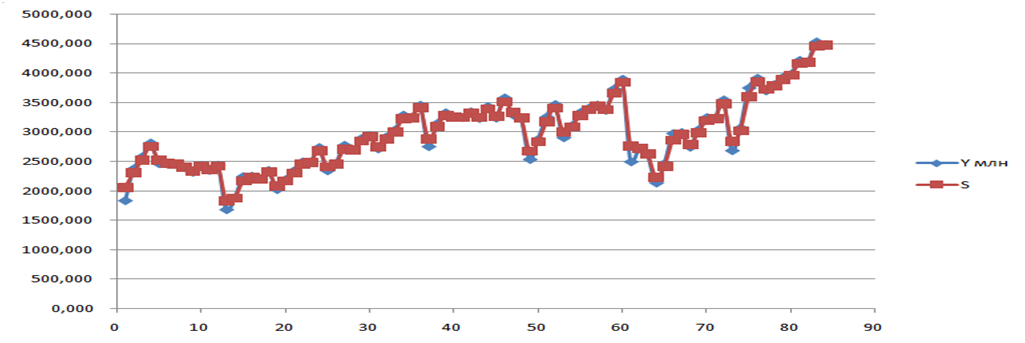
Рис.3. Графики исходного и экспоненциально сглаженного ряда

С помощью модели экспоненциального сглаживания вычислим прогнозное значение на январь 2022 года Y_прогн = 4477,586 млн. долл. США.

Исследуя график данного ряда (рис.3), имеем выраженную линейную тенденцию.В практике статичстического прогнозирования для отображения развития в виде линейной тенденции используют модели Брауна и Хольта.

Модель линейного роста для расчета прогноза имеет вид:

ytτ= a1,t+ a2,tτ (2)

где ytτ – прогноз, сделанный на τ единиц шагов вперед, τ – время упреждения прогноза.

Далее построим линейную адаптивную модель Брауна для нашего ряда с целью прогнозирования, используя формулу (2). С помощью метода наименьших квадратов для линейной аппроксимации данного ряда оценим значение параметров a_1,0 и a_2,0[3]. Применим аналитическое выравнивание, используя программный продукт MS EXCEL пакет «Анализ данных». Получим уравнение вида:

y(t) = 2164,45 + 18,76t

Тогда a_1,0= 2164,45 и a_2,0= 18,76. Используя эти значения параметров а₁и а₂, которые соответствуют моменту времени t = 0, находим начальные значения экспоненциальных средних:

S₀⁽¹⁾ = a_1,0- βα a_2,0 = 2159,763,

S₀⁽²⁾ = a_1,0- 2βα a_2,0= 2155,075,

где α = 0,8 и β = 0,2.Экспоненциальные средние вычислим по формулам:

S₁⁽¹⁾ = αy_t + βS_t-1⁽¹⁾,

S₁⁽²⁾ = αS_t⁽¹⁾ + βS_t-1⁽²⁾, (3)

С учетом выбранных значений параметров сглаживания и вычисленных экспоненциальных средних (см.(3)) корректируем параметры модели (2) a_1,_t и a_2,_tпо следующим формулам:

a_1,t = 2S_t⁽¹⁾ - S_t⁽²⁾,

a_2,t = αβ (S_t⁽¹⁾ - S_t⁽²⁾). (4)

Таблица 3

Расчетные значения по экспоненциальной средней

S_t⁽¹⁾	S_t⁽²⁾	a_1,t	a_2,t	Y_теор
1893,679	1945,958	1841,400	-209,117	1632,283
2273,965	2208,364	2339,566	262,405	2601,971
2511,701	2451,034	2572,369	242,670	2815,039
2747,548	2688,245	2806,851	237,212	3044,063
2514,458	2549,215	2479,700	-139,030	2340,671
2461,004	2478,646	2443,361	-70,569	2372,792
2449,547	2455,367	2443,727	-23,279	2420,448
2401,199	2412,033	2390,366	-43,334	2347,032
2327,433	2344,353	2310,513	-67,680	2242,833
2406,638	2394,181	2419,095	49,828	2468,923
2354,313	2362,286	2346,339	-31,895	2314,445
2415,702	2405,019	2426,385	42,732	2469,117
1823,435	1939,752	1707,118	-465,267	1241,851
1871,699	1885,310	1858,089	-54,442	1803,647
2163,440	2107,814	2219,066	222,504	2441,570
2228,152	2204,084	2252,219	96,270	2348,490
2199,429	2200,360	2198,497	-3,725	2194,773
2312,787	2290,301	2335,272	89,942	2425,214
2074,582	2117,726	2031,438	-172,576	1858,862
2164,191	2154,898	2173,485	37,173	2210,657
2299,098	2270,258	2327,938	115,360	2443,299
2447,436	2412,001	2482,872	141,742	2624,615
2475,756	2463,005	2488,507	51,004	2539,510
2678,594	2635,476	2721,711	172,471	2894,183
2403,072	2449,553	2356,591	-185,923	2170,669
2451,998	2451,509	2452,487	1,956	2454,443
2704,644	2654,017	2755,271	202,508	2957,779
2691,513	2684,014	2699,012	29,997	2729,009
2843,309	2811,450	2875,169	127,437	3002,605
2917,007	2895,896	2938,118	84,445	3022,563
2747,499	2777,178	2717,819	-118,717	2599,102
2878,123	2857,934	2898,312	80,756	2979,069
2998,901	2970,707	3027,094	112,773	3139,867
3222,219	3171,917	3272,522	201,209	3473,731
3239,424	3225,922	3252,925	54,006	3306,931
3405,982	3369,970	3441,994	144,048	3586,042
2876,498	2975,192	2777,803	-394,778	2383,025
3084,568	3062,692	3106,443	87,500	3193,943
3271,265	3229,550	3312,979	166,858	3479,837
3246,098	3242,788	3249,408	13,238	3262,646
3239,981	3240,542	3239,419	-2,246	3237,173
3316,899	3301,627	3332,170	61,085	3393,255
3240,947	3253,083	3228,811	-48,544	3180,267
3388,761	3361,625	3415,896	108,542	3524,438
3260,997	3281,123	3240,872	-80,502	3160,370
3509,177	3463,566	3554,787	182,443	3737,230
3327,337	3354,582	3300,091	-108,983	3191,107
3233,890	3258,028	3209,751	-96,554	3113,197
2668,481	2786,391	2550,572	-471,638	2078,934
2829,095	2820,554	2837,636	34,164	2871,799
3163,958	3095,277	3232,638	274,723	3507,361
3399,789	3338,886	3460,691	243,609	3704,300
2996,692	3065,131	2928,253	-273,755	2654,498
3081,317	3078,080	3084,555	12,949	3097,504
3277,193	3237,370	3317,015	159,290	3476,305
3376,137	3348,384	3403,890	111,013	3514,904
3434,548	3417,315	3451,780	68,931	3520,712
3374,644	3383,178	3366,110	-34,136	3331,974
3652,594	3598,711	3706,477	215,532	3922,009
3840,992	3792,536	3889,448	193,825	4083,273
2757,549	2964,546	2550,551	-827,989	1722,562
2717,856	2767,194	2668,519	-197,352	2471,167
2623,877	2652,540	2595,213	-114,654	2480,559
2225,800	2311,148	2140,452	-341,392	1799,060
2414,411	2393,758	2435,064	82,610	2517,674
2856,880	2764,256	2949,505	370,498	3320,002
2959,054	2920,094	2998,013	155,838	3153,851
2780,009	2808,026	2751,992	-112,068	2639,924
2982,261	2947,414	3017,108	139,388	3156,495
3188,282	3140,108	3236,455	192,694	3429,149
3219,478	3203,604	3235,353	63,496	3298,849
3474,710	3420,489	3528,931	216,884	3745,815
2836,191	2953,050	2719,331	-467,438	2251,893
3016,677	3003,952	3029,403	50,902	3080,304
3595,771	3477,407	3714,135	473,456	4187,591
3843,176	3770,023	3916,330	292,615	4208,946
3721,769	3731,420	3712,119	-38,603	3673,516
3783,721	3773,261	3794,181	41,841	3836,022
3891,011	3867,461	3914,561	94,200	4008,761
3958,959	3940,660	3977,259	73,199	4050,458
4157,772	4114,349	4201,194	173,690	4374,884
4178,141	4165,383	4190,900	51,033	4241,933
4453,095	4395,553	4510,638	230,170	4740,807
4473,504	4457,914	4489,095	62,361	4551,456

Используя (4), находим скорретированные параметры линейного тренда:

а1,84 = 4489,095; а2,84 = 62,361.

По модели (2) со скорректированными параметрами находим прогноз на январь 2022 года равен 4551,456 млн. долл. США.

Приведем графики теоретических и фактических значений ряда объемов товарооборота России со странами ЕАЭС в стоимостнгом выражении (рис.4).

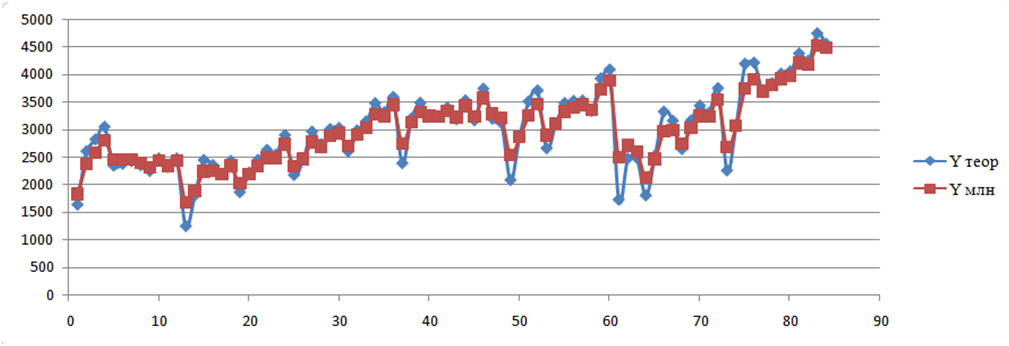
Рис.4. Графики теоретических и фактических уровней ряда

Также вычислим долю ошибки представленных выше расчетов, которая составила в процентном формате 9%. Оставшаяся часть 91% ― доля дисперсии уровней временного ряда, объясненная моделью (2).

В рамках проведенного эконометрического моделирования стоимостных объемов товарооборота РФ со странами ЕАЭС двумя способами получены прогнозные значения на январь 2022 года. Так, при использовании модели экспоненциального сглаживания прогнозное значение объема товарооборота составило 4477,586 млн. долл. США, а в случае применения модели Брауна ― 4613,817 млн. долл. США. По данным таможенной статистики, опубликованным ФТС России за январь 2022 года (до введения ограничений, связанных с конфиденциальностью внешнетрговой статистики), товарооборот РФ во взаимной торговле со странами ЕАЭС составил 4464,7 млн. долл. США [4]. Соответственно, можно оцениить точность построенных прогнозных моделей, так, относительное отклонение модели экспоненциального сглаживания составило 0,31%, а модели Брауна―3,36%.

Следовательно, на основании представленных данных можно сделать вывод, что прогнозное значение адаптивной модели с использованием экспоненциального сглаживания оказалось наиболее близким к рельным данным.

Список литературы

1. Официальный сайт ЕЭК [Электронный ресурс]. URL: https://eec.eaeunion.org/

2. Цвиль М.М. Анализ временных рядов и прогнозирование // учебное пособие. Ростов-на-Дону: Российская таможенная академия Ростовский филиал. 2016. – 135 с.

3. Лукашин Ю.П. Адаптивные методы краткосрочного прогнозирования временных рядов // учебное пособие. – Москва: Финансы и статистика - М. 2003. 416 с.

4. Официальный сайт ФТС [Электронный ресурс].URL: https://customs.gov.ru/

Рецензии

1. Оценка объемов товарооборота России со странами ЕАЭС
Авторы: Кудрявцев Олег Евгеньевич

Отправить рукопись Скачать PDF
Текст

Цитировать

Цитирований:

Подтверждение

Регистрация